9.50

Highway engineers in Ohio are painting white stripes on a highway. The stripes are supposed to be approximately 10 feet long. However, because of the machine, the operator, and the motion of the vehicle carrying the equipment, considerable variation occurs among the stripe lengths. Engineers claim that the variance of stripes is not more than 16 inches. Use the sample lengths given here from 12 measured stripes to test the variance claim. Assume stripe length is normally distributed. Let α = .05.

 

Stripe Lengths in Feet

10.3	9.4	9.8	10.1
9.2	10.4	10.7	9.9
9.3	9.8	10.5	10.4

 

σ² = 16inches

n = 12

α = .05

 

Step #1: Hypothesis.

H₀: σ² = 16

H_a: σ² < 16

 

This is a one-tailed test

 

 

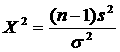
Step #3: α = .05

Step #4: df = 12 -1 = 11

 

From Table A.8:

 

Step #6: s² = ?

Stripe Lengths in Inches

123.6	112.8	117.6	121.2
110.4	124.8	128.4	118.8
111.6	117.6	126.0	124.8

 

From excel calculation: s² = 35.825

The observed chi-square value is calculated as:

 

 

 

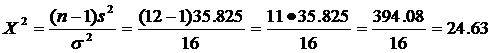
Step #7: Action.

 

This observed chi-square value is in the Rejection Region because:

 

 

The null hypothesis is REJECTED. The results indicate, with 95% confidence that the sample variance, σ² is greater than 16 inches. Quality control of the painters needs to be reviewed and improved.